Enchanted Forest Wedding {07.28.18}
On July 28, 2018, under the warm summer sun and beneath a canopy of trees, Micah and Francesca tied the knot in the most personal and emotional backyard enchanted forest wedding I’ve ever had the joy of photographing. And trust me, this one stayed with me — not because of extravagant florals or elaborate décor (though, yes, there were many dreamy details), but because of the deep love, family ties, and handmade touches that made this day feel like stepping into a storybook.
From scotland to china to connecticut…
Francesca is one of those rare souls who carries the stories of many places. Originally from Scotland, she spent her childhood between there and Italy — and she’s got that worldly, creative spirit to show for it. She met Micah in India while he was teaching in China (yes, really), and that initial spark grew into a love that spanned oceans and time zones.
Eventually, Francesca moved to China to be with Micah, and from there, their story started to unfold more tangibly — building a life together, planning a wedding, and dreaming of their future. Naturally, their wedding became a melting pot of the people and places that shaped them. Guests traveled in from Scotland, Australia, India, and all across the U.S. — each person a special part of their journey.
Turning a backyard into a woodland wedding dream…
When I visited their ceremony site a few weeks before the wedding, I found them literally in the dirt — pulling weeds, planting grass, and transforming Micah’s childhood backyard into the enchanted forest setting they had envisioned. And let me tell you — they pulled it off.
Imagine this: A sun-dappled clearing in the woods, with oriental rugs creating a boho-style aisle. Mismatched china set at long farm tables under the trees. Breezy florals, hand-tied with Scottish tartan ribbons. It was intimate, relaxed, and filled with soul.
Meaningful details + heirloom touches…
Francesca and Micah brought in so many personal and family-centered elements. Francesca wore a ring that had belonged to Micah’s great-grandmother (and his mom, too). Her opal earrings were her mother’s, and she wore a garter handmade by her bridesmaid. The night before the wedding, Micah gifted her a vintage watch that had belonged to his great-aunt. He also wore a pin inside his vest with a photo of his grandfather — such a special way to keep loved ones close.
And the Scottish details? Iconic. A handfasting ceremony with a Mackenzie tartan ribbon. Bagpipes playing as they recessed down the aisle. Francesca’s father and other guests wore kilts, and Micah’s vest matched the tartan of her bouquet ribbons. Every detail honored their roots while creating something entirely unique to them.
A wedding built with love (+ a little sweat!)…
From the hand-built dance floor (yes, they built that too) to the homemade chocolate favors created by close friends, everything about this wedding was intentional. Friends and family helped with dinner service, bartending, and even valet. It felt like one big group hug disguised as a wedding — and I adored every second of it.
The ceremony itself was filled with surprise and sentiment. Their families had secretly organized a series of readings, with guests standing up one at a time to share different “chapters” of Francesca and Micah’s love story. Cue the tears. Francesca’s sister sang both What a Wonderful World and Amazing Grace — and not a dry eye in sight.
The speeches? Hysterical and heartfelt. Francesca’s dad joked about being “married to the MOB,” but also praised his daughter’s resilience, saying, “She may be tiny, but she punches above her weight — so watch out, Micah!” (Dead. I was laughing and crying.)
Dancing in the rain – literally…
After a long, beautiful day of sunshine and happy tears, the skies opened up. And what did they do? Covered the equipment in plastic and kept the party going. Everyone danced in the rain on that handmade floor, laughing and soaked and so full of joy.
Micah + Francesca, I still think about your enchanted forest wedding day and how beautifully you wove your story into every single moment. Your wedding wasn’t just a celebration — it was a love letter to your past, present, and future. I’m so honored I got to be the one to capture it.
All my love.
Vendors:
Photography: Love, Sunday
Catering: Red Diamond Pizza Truck
Rentals: Taylor Rentals
Bride wore: Martina Liana from Alexandra’s Bridal Boutique





































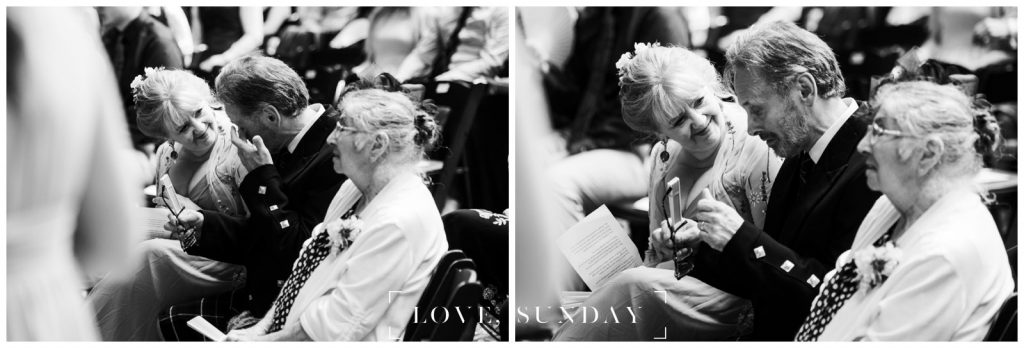







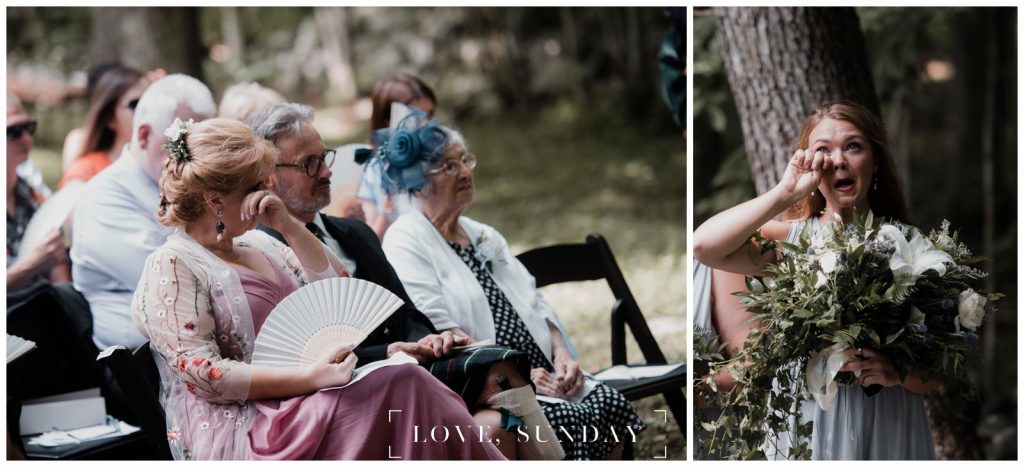



















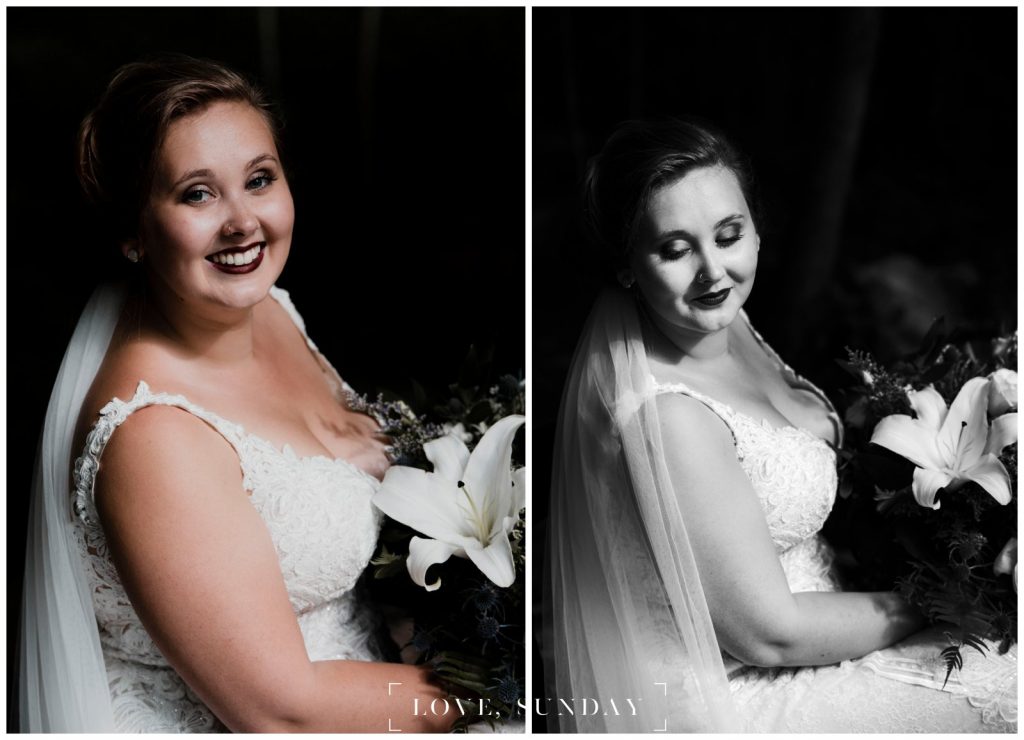






















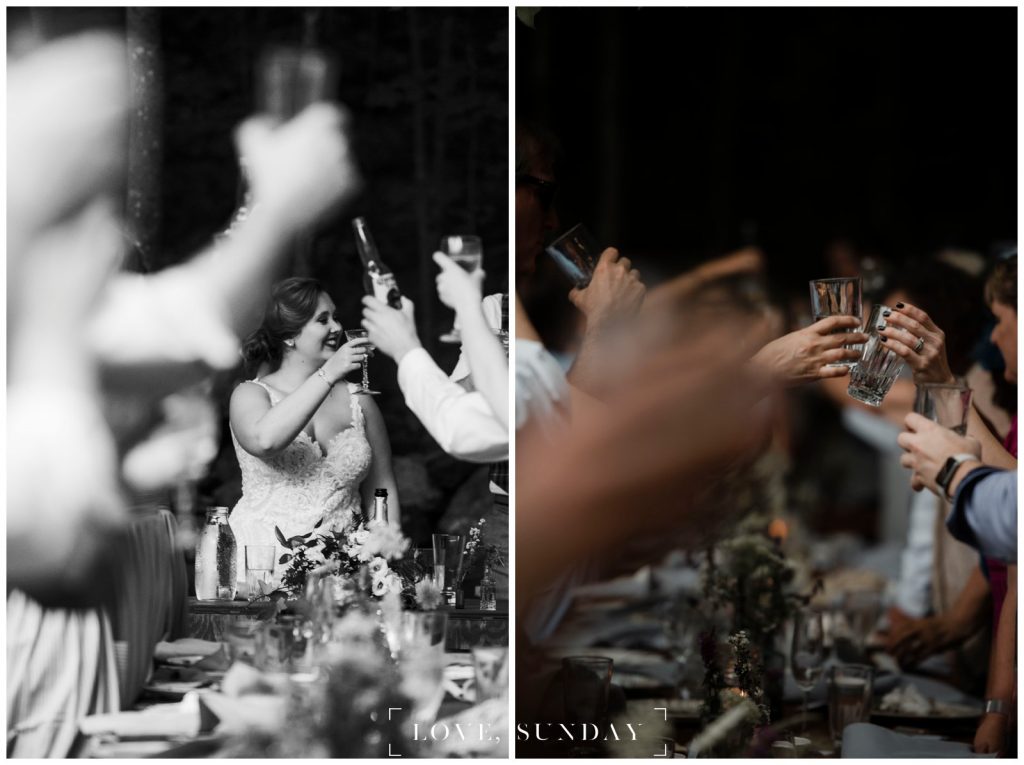
















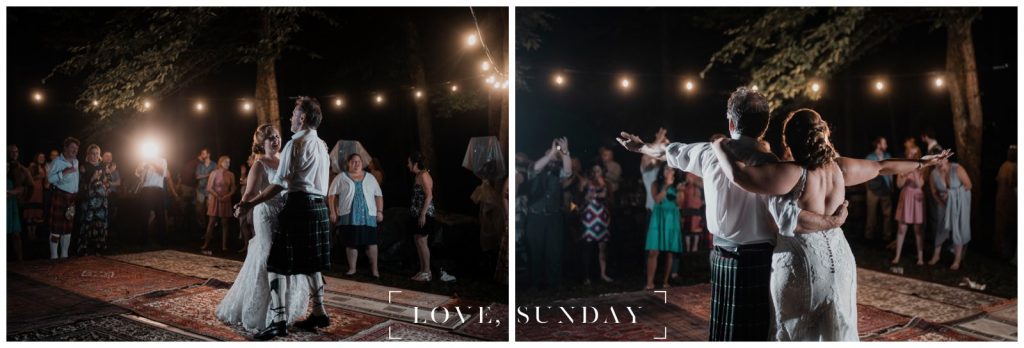






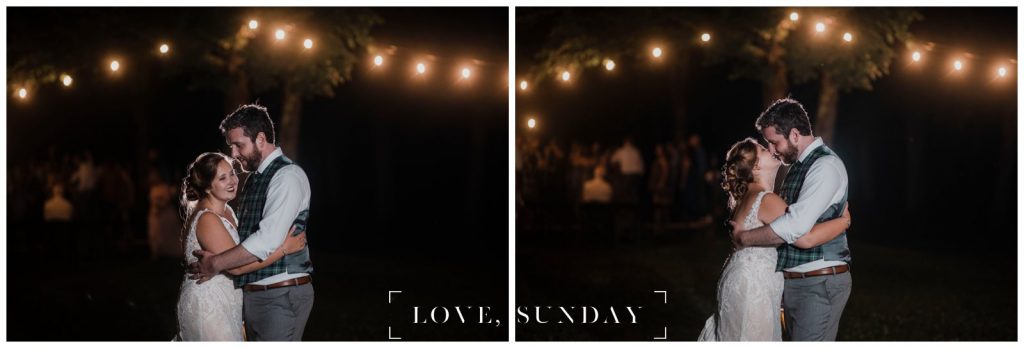


Comments